平均を知らない人はいない。平均を計算した時、「まあこんなもんだろうな」と思う時と、「あのデータだけ飛び抜けていたからなあ」と、偏ったデータを思い浮かべる時がある場合では、同じく平均を平均として扱うことに疑問が生じる。
例外値の影響を大きく受ける時には、中央値をつかう
中央値(メディアン) = すべてのデータを小さい方から並べた時、その真ん中にくる値
※データ数が偶数の場合は、真ん中の2つ足して2で割った値を中央値とする。
データで同じ値が複数あるなど特徴がある時には、最頻値(モード)も考えてみる。
データが平均の上下にたくさん分布している時
バラツキの平均を求める = 分散
- データの平均を出す
- 平均とデータの差を出す(これを偏差という)
- 偏差を2乗する
- 偏差の2乗をデータ数で割る = 分散
分散の値が小さいほどバラツキが小さく、平均値の周辺にデータが分布している。
分散のデータ分布から基準値となる値を求めたい
仮説 バラツキが他所より大きいと問題が潜んでいる(流れ作業を行う工場)
そこで標準偏差を求める
標準偏差 = √分散( 関数 =sqrt(数値orセル))
※平均が同じものを比べる時に有効
規模がちがう為、比べる値に大きな差がある。項目がちがう為、単位が異なる。これらの条件を比較する方法として変動係数をつかう。
変動係数 = 標準偏差÷平均
単位が異なっても変動係数にすることで比べることができる。
正規分布
標準偏差の値が小さい = 平均の近くにデータが集中する(山の高いグラフになる)
正規分布曲線
曲線の中心 = 平均 = 中央値 = 最頻値
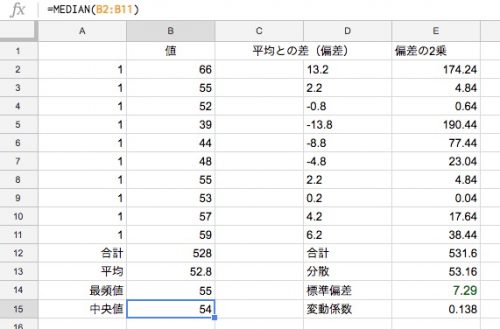
例として、上の表の「値」を「売上個数」とし、残り2ヶ月で製造中止となる部品の仕入れ数は何個が適切なのか考えます。(現在の自社在庫はゼロと仮定)
標準偏差を知らないとしたら、平均約53、最頻値が55だから55でどうかとなる可能性がある。しかし、66や57の月もあるので足りない可能性もある。
66個以上売れる確率は?
(66-平均値52.8)÷標準偏差7.29=1.81
1.81を標準正規分布表で見てみると 0.4649
https://goo.gl/zU9WVt
正規分布曲線は左右対称なので、右側全部で50%
そこから46.49%を引いた数が66個以上売れる確率です。
50-46.49=3.51%
これが60個以上売れる確率だと16.11%になりました。なんか微妙に売れそうな気がします。
5%以下の確率なら安心ということで仕入れは更に計算して65個(4.75%の確率)にすることにしました。
ちょっと疑問は残りますが、これまで過剰に購入して廃棄したり、不足して納期に間に合わないを考えると、標準偏差を考慮する以前よりは値に説得力があるのかなと思ったりします。